Caractérisation de l'orthocentre

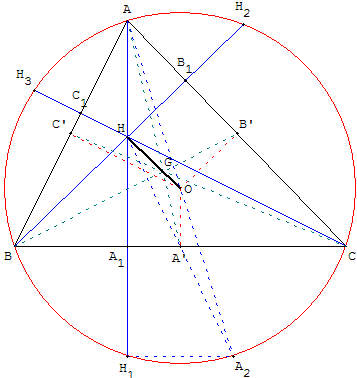
Soit ABC un triangle non équilatéral, O le centre du cercle circonscrit, G le centre de gravité et H l'orthocentre.
On cherche à caractériser le point M tel que .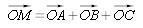
Caractérisation de l'orthocentre
Soit M le point tel que : 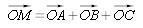, on en déduit l'égalité : 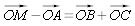et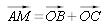
On note A' le milieu de [BC]. Le triangle BOC est isocèle en O donc 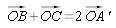d'où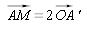

Le vecteur 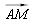est colinéaire à 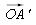qui est un vecteur directeur de la médiatrice de [BC]. On en déduit que (AM), parallèle à (OA’), est perpendiculaire à (BC) ; c'est la hauteur (AA1) du triangle.
On montre de même que (BM) est aussi la deuxième hauteur (BB1) et on conclut que le point M, intersection de deux hauteurs, est l'orthocentre H de ABC.

Relation d'Euler
En remplaçant M par H on obtient la relation vectorielle 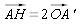et la relation d'Euler .
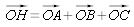La définition vectorielle du centre de gravité permet d'écrire : 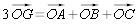donc .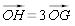
Les points O, G et H sont alignés sur une droite dite droite d'Euler (1707-1783) et GH = 2 GO (relation d'Euler).

Symétriques de l'orthocentre
Il vient d'être démontré que .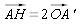
Si A2 est le symétrique de A par rapport à O, dans le triangle AHA2, (OA’) passant par le milieu O du diamètre [AA2] et parallèle au côté (AH) est la droite des milieux du triangle. A' est le milieu de [HA2] et A2 est le symétrique de H par rapport à A'.
Les symétriques de l'orthocentre par rapport aux milieux des côtés du triangle sont situés sur le cercle circonscrit au triangle.

[AA2] étant un diamètre, le triangle AH1A2, inscrit dans un demi-cercle est rectangle. La droite (BC), perpendiculaire à (AH1) est parallèle à (H1A2) et passe par le milieu A' de [HA2].
Dans le triangle HH1A2, (A1A’) est la droite des milieux, A1 est milieu de [HH1]. (HH) étant perpendiculaire à (BC), H1 est le symétrique de H par rapport à (BC).
Les symétriques de l'orthocentre par rapport aux côtés du triangle sont situés sur le cercle circonscrit au triangle.